Generating a Minecraft map as website
I recently started playing Minecraft again with my son, and it was a ton of fun playing together, and also rediscovering all the changes in the game since I played last some years ago.
One time I was exploring the world for a bit and then died (bloody skeletons) leaving all my stuff in the middle of nowhere. After trying to find the place where I'd died, I remembered that there used to be a server mod which would generate a 2D overview of the world, so it was easier to see where things actually were, especially for someone like me who somethimes struggles with orientation.
As I am running a local, vanilla server JAR on my laptop just for the time that we are playing, I didn't want to introduce any mods, so I looked for a way to generate a map just from the world files that Minecraft had generated, and found Unmined.
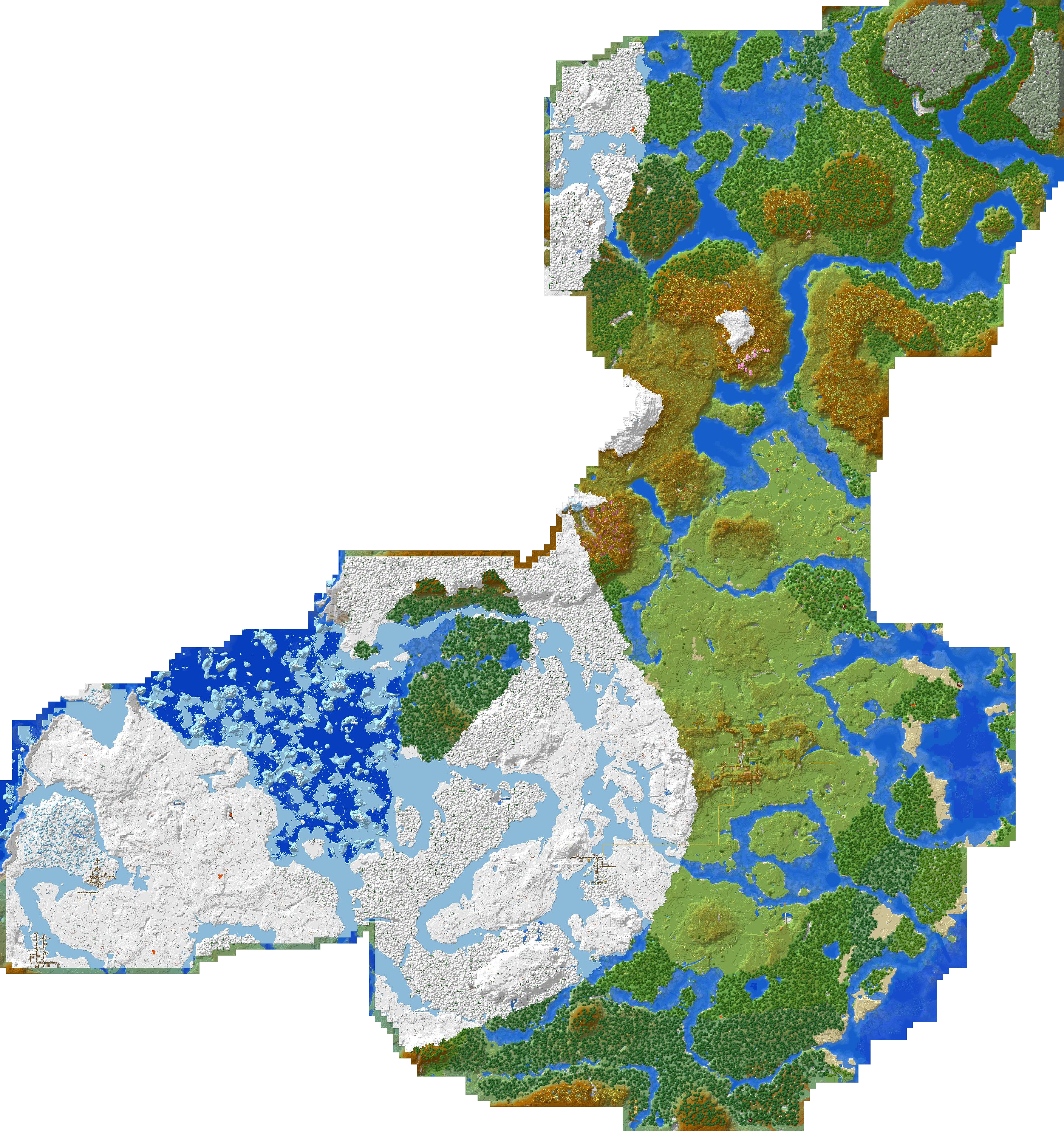
With the CLI version of Unmined and a simple command (./unmined-cli image render --world="world" --output="./map.png"), it is possible to generate images like this:
Now have the whole Minecraft world as an image is already pretty cool, but zooming is a bit tedious and also the coordinates are not showing, making it a bit difficult to use besides the game.
Luckily, there's also a web parameter for the CLI, which will generate a Google Maps-like tile map, where on lower zoom levels, tiles are dynamically fetched and shown. Like this:
The map above was generated with
./unmined-cli web render --world="world" --output="generated-map" --zoomin=2
The --zoomin-parameter specifies how far the maximum zoom depth should be, and with 2 it already generated around 3'000 files. Setting it to --zoomin=3 would generate around 12k files.
Highlights
Some cool things to discover on the map above:
 Cherry blossom trees
Cherry blossom trees
 Minecart tracks showing up in yellow
Minecart tracks showing up in yellow
 Village
Village
 Abandoned portal (?)
Abandoned portal (?)
Happy mining!