kleemans.ch

Draw on the canvas and hit start to begin the simulation!

Conway's Game of Life is a simulation of simple life forms, known as cells, where cells either are alive (black cells) or dead (white cells). Cells are placed next to each other in a grid like above, and a state (or generation) can be calculated by knowing how the grid was before.

Being a type of "cellular automaton", the Game of Life follows a simple set of rules, which decide how the next generation looks like:

1. Any live cell with two or three live neighbours survives.
2. Any dead cell with three live neighbours becomes a live cell.
3. All other live cells die in the next generation. Similarly, all other dead cells stay dead.

This can be written as follows:

if neighbor_count(cell) == 3 or (cell == alive and neighbor_count(cell) == 2):
    cell_next = alive
else:
    cell_next = dead

The fascinating part is, that with these simple rules, unexpected patterns can emerge, and as it turned out, the Game of Life is even Turing complete.

There are many patterns which are small enough so they can be easily drawn by hand, and have unexpected outcomes. One such example is the Glider:

Another example of a pattern which first emerges into something like a flower and then later stabilizes:

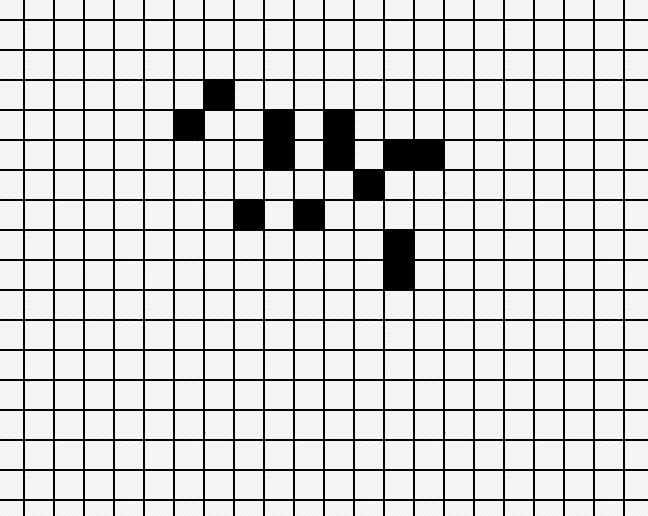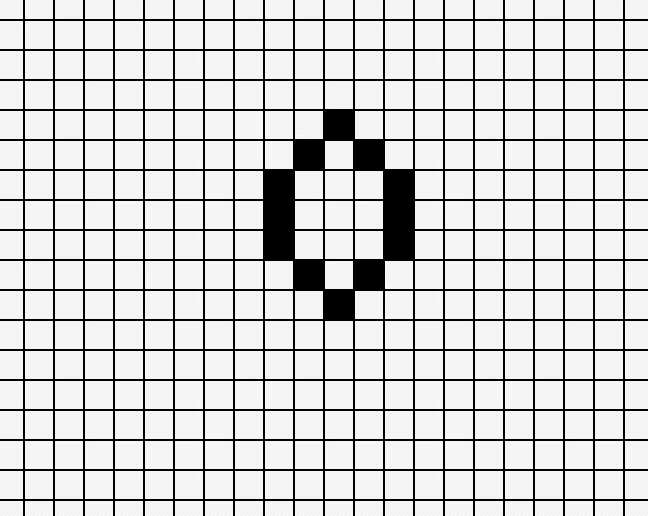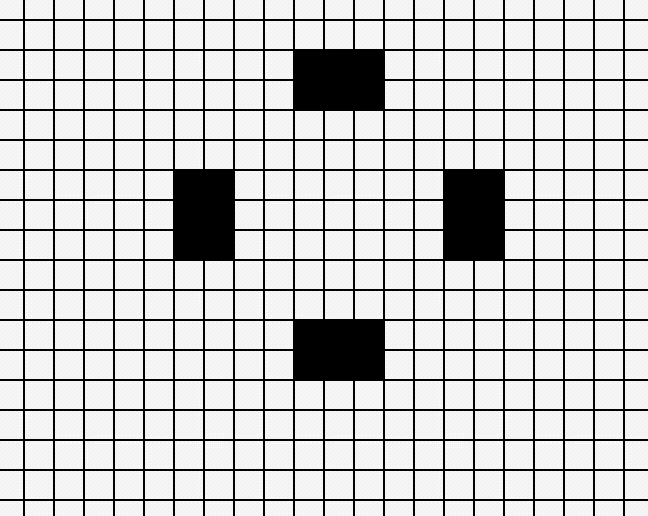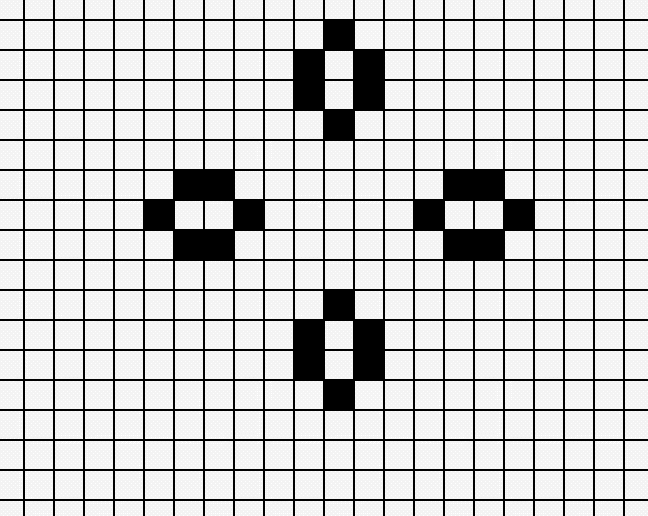
These are just two really small examples - with something called Glider guns, it is possible to produce gliders, which in turn can be used for tape-like programming.

There are also really powerful programs like Golly, which allow for extremely fast calculation and even jumping to certain generations.

The simulation at the top of this post was made with P5.js and TypeScript. You can find the source code on my Github.

Thanks for reading!