kleemans.ch

I recently learned about Hitori - a japanese logic puzzle from Nikoli, who also invented Sudoku - and became a little bit addicted to them. I used to solve Sudokus now and then, but I've always loved logic puzzles in general, so it was just a question of time before I stumbled onto Hitori.

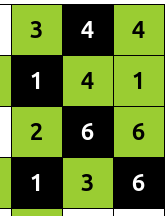
Here's an example of a puzzle with solution:

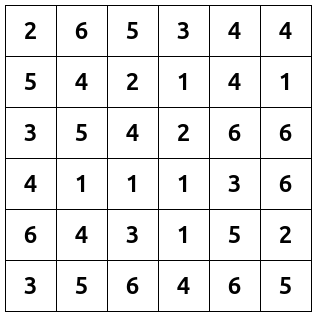
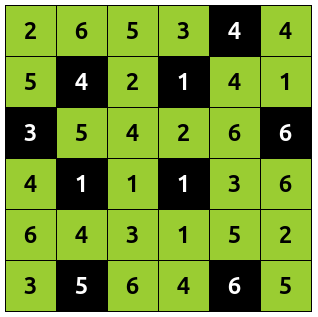
The goal is to color cells with black until all rules are satisfied. An additional color can be used (like green here) to mark correct numbers.

The 3 rules are:

• No row or column can have more than one occurrence of any given number. For example, in the initial grid, the top rows contains two 4s, so one of them must be marked black.
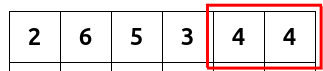
• Black cells cannot be horizontally or vertically adjacent. For example, this would be invalid:
• All white cells must be all connected to each other (horizontally or vertically). This means, no cells or cell groups can be isolated, we'll look at an example below.

Even though it seems similar to Sudoku at first glance, I find it much more intuitive to solve, because some parts rely more on visual pattern recognition than in Sudoku. In Sudoku, I sometimes find myself iterating through the numbers to see what I didn't spot, a rather tedious process.

Example 1: In the upper right corner of the puzzle above, after knowing that the 4 is black, we have the following scenario:

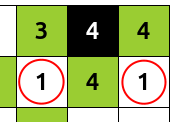
We have two 1s, so one of them must be black. But which one? As the 4 in the upper right corner must be connected to the other cells, we know the 1 below it can not be black, so it must be the other.

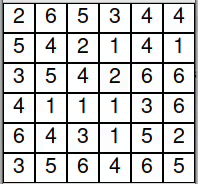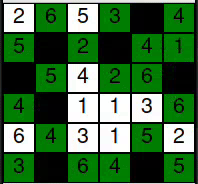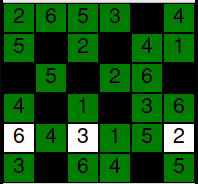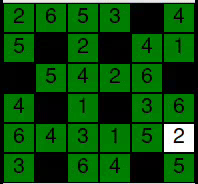
Example 2: Just below there is another example, which requires slightly more thought. We have 3 adjacent 6s and have to find out which ones we have to color black:

Now if we would pick either of the diagonal 6s and mark it black, the 6 in the upper right would have to be green, and the other one would need to be black. This would lead to the following situation:

Which isolates a part of the grid and is therefore invalid, so the two diagonal 6s must be green instead. Neat, right?

Additionally, Hitori will give you these nice patterns when they are solved:

Writing a solver

Similar to my Sudoku solver and sudoku-solver.ch, constraint propagation (see Peter Norvig's great post about it) works also very well here.

We can work with just 2 constraints here, followed directly from the rules:

1. If a cell is black, the adjacent cells must be white.
2. If a cell is white, all other cells in that row/col must be black.

The algorithm is then the following:

• Pick an undecided cell
• For both states (black and white), try that color and propagate
• With the new grid state, repeat.

This leads very quickly to either an unsolvable puzzle or returns the solution, and can be solved in an elegant way using recursion.

Example Python code:

def solve_recurse(hitori: Hitori):
    guess = pick_undecided_cell() # Pick next cell candidate
    for state in [State.BLACK, State.WHITE]:
        hitori_new = Hitori.clone(hitori)
        # Set state and propagate
        hitori_new.mark(guess, state)
        hitori.propagate()
        if hitori.is_solved():
            return hitori_new
        elif hitori_new.is_valid():
            Solver.solve_recurse(hitori_new)

Happy puzzling!